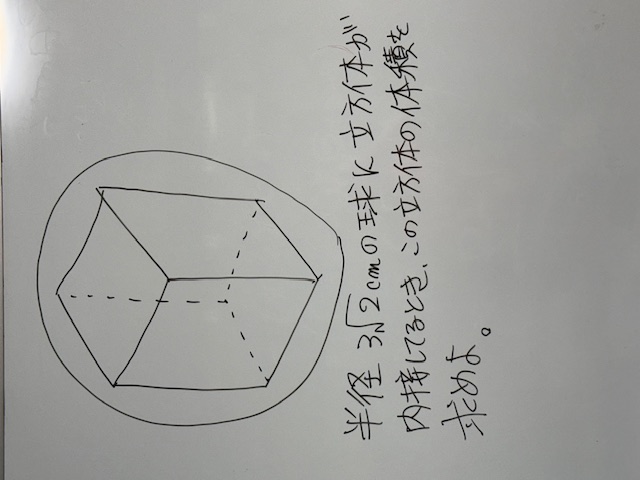
中3数学 · 30日 6月 2025
三平方の定理で立方体や直方体の対角線の長さを求めることができますよね。このことを思い出せた生徒さんは勝ちです。今回は立方体、つまり1辺の長さはすべて同じなのでとりあえずx(エックス)にして計算しちゃいましょう。よって求める体積は48√6立方cmなります。あってたかな?
中3数学 · 27日 6月 2025
一瞬、「はっ?」と戸惑いますが、冷静に考えると意外とわかっちゃったりします。実際、塾の中1に見せたところ、それほど絶望せず、すぐに自分で考え始めました。問題文を読み直すと、半径が与えられてて、しかも球に内接しているのは立方体です。これらのことから中1生女子は、あることに気が付きました(えらい!)。あとは、中3・高1の三平方の定理を知っていればすぐに解けます。とりあえず、適当に内接してる接点に名前(アルファベット)をふってあげましょう。そうすると計算しやすくなりますね。今回のポイントは、問題を見た時に心折られず、まずは「どういう状態なのか」を冷静に考えてみる事でした。まずは自分の力で挑戦してみてください。
大島学習塾 · 25日 6月 2025
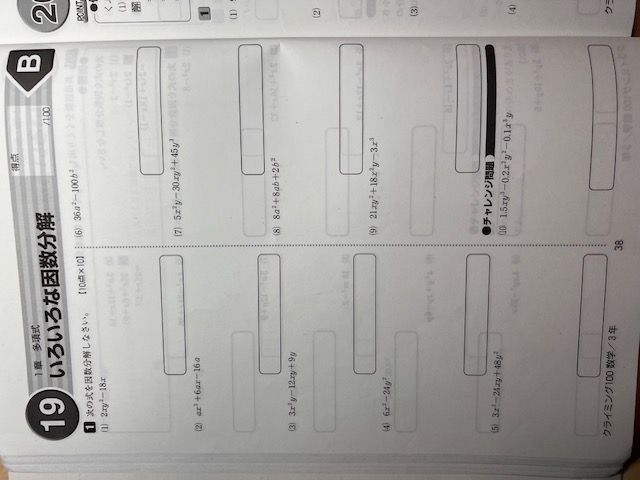
当塾には、集団コースと、個別コースがありますが、集団コースでも特に数学は個の開きが大きいので、塾生は各自の理解度に沿った個別の問題集を使用しております。なので、集団コースですが、数学の時間は個別対応の時間帯もあります。本日ご紹介するテキストは←こちらです。1ページに5~10問。基本的問題のAと難易度が上がったBの2ページ構成。この問題集は、平均点あたりから、上位層の背中位を狙いたい生徒さんにピッタリです。問題数がそれ程多くないので、飽きがこずページ数を稼げます。つまり達成感が得られるのが良い点です。Titleどおり100(ページ数なら200)ありますので、これをcompleteできたら数学が得意科目になってきた感を得るでしょう。学校のワークには答えを書き込んでしまいますので、ほとんどの生徒さんは、二度目はやりません。なので塾ではとある生徒さんにクライミング100を解かせてみます。これが完璧になったら、ちょっと楽しみです。次は新中学問題集・発展編で上層へステップアップかな。
中2理科 · 23日 6月 2025
これも良く出る問題です。空気中でマグネシウムを加熱し、質量を計ったら、少し増えてた。でも完全には反応してなかったパターンです。意味が分からないときは、実際に絵にかいてみましょう。図は下手でもいいんです。自分がわかればそれでOK。ここで必要な知識は、マグネシウムと酸素と酸化マグネシウムの反応する質量比を覚えてますか、ということです。酸化マグネシウムのパターンだけでなく、銅:酸素:酸化銅のもスラスラ答えられるように練習しときましょう。
中3数学 · 19日 6月 2025
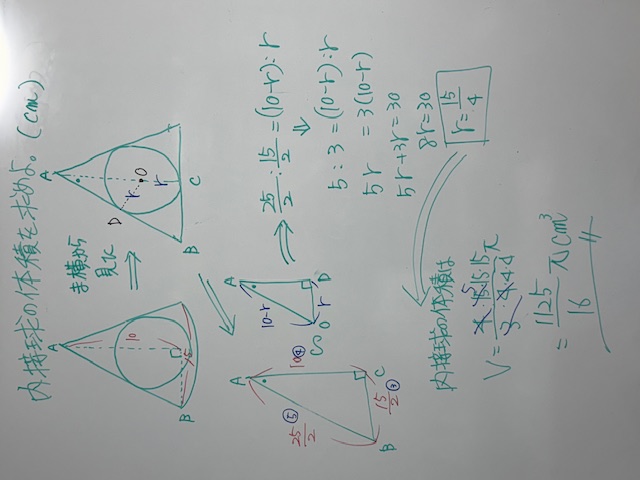
立体をそのまま考えても難しそうですよね。なので、真正面(ま横)から見た平面図で考えてみましょう。そこに、半径rを書き込んであげると・・・塾でいつも言ってますよね、接線を見たら接点の問題だ、と。接点を見たら、中心と結んであげるといいことがある=垂直に交わってる。この流れでしたね。△ABCと△AODは相似だと気が付いたあなたは素晴らしい。ここまで来たら、あとは比べてあげると求めたい半径rが求まります。最後に内接球の体積を求めるので、ここからは頭は使いません。ただの作業です。文字を書くだけ。塾で口酸っぱく言ってます、計算したら負けですよ・笑。頭使っちゃダメです。何も考えずに、ただ手を動かすだけ。いいですか。最後は約分祭り。あなたの答え、あってましたか?お疲れさまでした。中学生は、これをスラスラ解けるように練習しといてください。
中3数学 · 17日 6月 2025
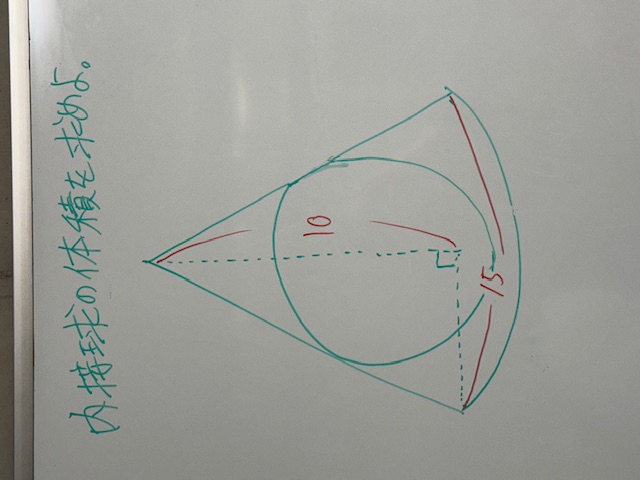
これは、某中学(中3)の数学のプリントの類題です。円錐の内接球の体積を求めるには、内接球の半径がわかればいいんですよね。では、半径を求めに行きましょう。中3生は、頑張って解いてみてください。ちなみに単位は cm です。
中3数学 · 15日 6月 2025
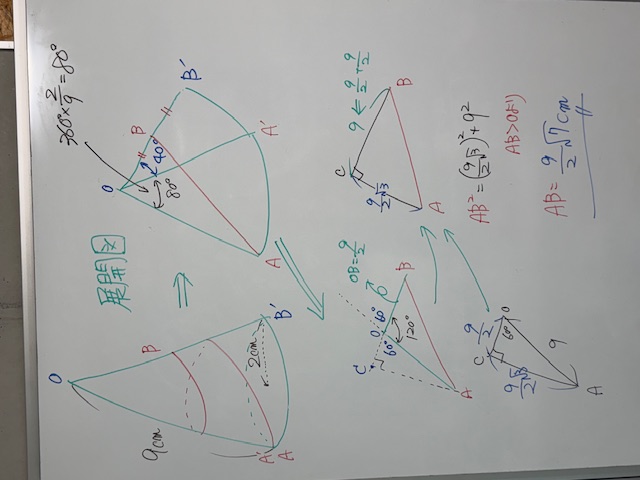
今回は展開図が書けるかどうかがカギです。終着点のBは母線OB’上にあるので1周半したと考えればいいでしょう。半周のびるから中心角も半分増える。120度になっちゃいますが、しかたないを受け止めて、とりあえずわかってることだけを展開図に書き込んでください。ここで、「こんなの難しい。出来っこない」と先読みして手が止まる生徒さん多いはずです。出来ないのは当然、だって難しい問題なんだから、と開き直って挑んでください。そこに突破口が見つかります。いいですか、先のことばかり考えてもダメ。今直面してる課題に知ってる知識だけでなんとか解けないかなと考えてみましょう。知ってる知識、直角三角形があったら三平方の定理が使える。このことですよね。角AOB120度があったら、その外角は60度です。あとは垂線ACを下ろしてあげたら・・・ほらね、なんか使えそうでしょ。ここから先の計算は、あなたに任せます。答え同じになりましたか?
中3数学 · 13日 6月 2025
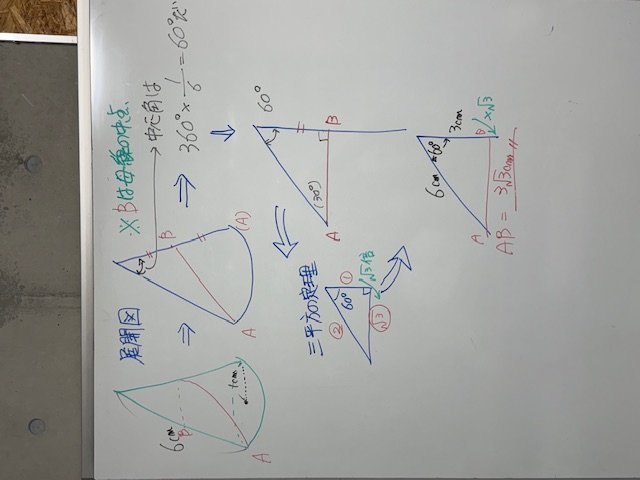
円錐上のひも到着地点Bの位置に着目してください。頂点と、出発地点Aを結ぶ母線上にありますよね。なので、展開図でも同じ辺上に位置(プロット)してあげましょう。しかも、※Bは母線上で、中点ですよ、とヒントもくれてます。ありがたく使わせていただきました。あとは、展開図の扇形の中心角の大きさを求めましょう。60度ですね。Bは母線の中点なので、ABは母線と垂直に交わります。つまり、90度もgetできました。ここまできたら、今得た60度と90度、そして母線の6cmの関係を考えたいので、展開図をもう一度眺めます。すると、直角三角形(しかも60度あり)が見えてきましたね。ここまで来たら、もう勝ちです。あとは、三平方の定理のしかも90度と60度のスペシャルバージョンにあてはめてあげると、ABの長さが出ます。自分の手でも解けるように、何度も何度も練習してください。今日できるようになっても、明日は忘れてる可能性大です。ちゃんとマスター出来たか明日も、確認のために再挑戦してみてください。無事解けたら、あなたは合格です。解けなかったら、また復習あるのみ。頑張ってくださひ。←あっ、嚙んじゃった
中3数学 · 10日 6月 2025
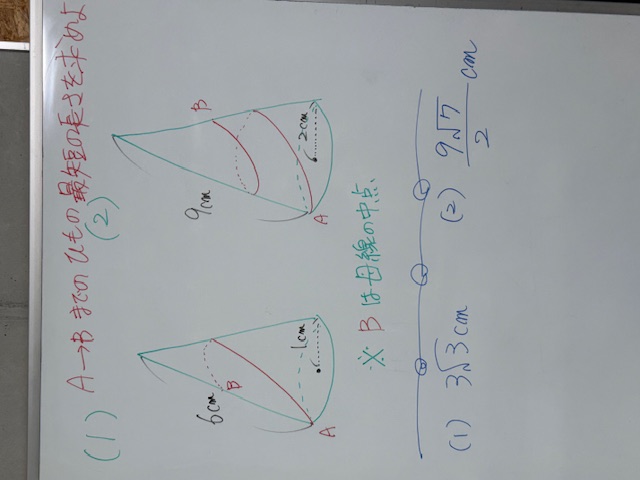
(1)は、すんなり解けると思います。問題なのが(2)ですよね。焦らず、落ち着いて、考えてみましょう。なぜ(1)で、こんなのを解かせたのか。だって(1)と(2)、なんとなく似てませんか。本問も「展開図で考える」です。パッと見、全然わからなくてもいいんです。そんな時は、「自分には無理無理」焦って解かなくていいんです「じゃぁ、どンな風になってるんだろう?」と小説を読む如くまるで他人事のように、興味津々で、展開図に落とし込んでとりあえず、実験してみましょう。最短距離のルートが見えましたか?(^^)
中3数学 · 09日 6月 2025
証明問題が苦手な生徒さん多いです。
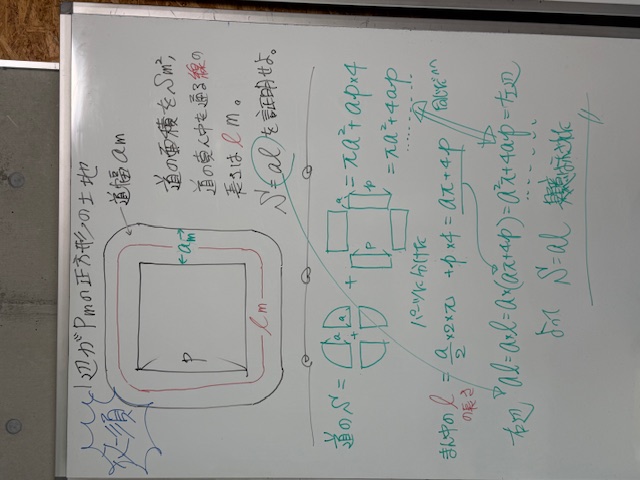
コツは、①左辺と右辺の両方をいじって(=変形させて)、その結果同じになった、同じでしょ□。あるいは、②左辺のみいじる=右辺、あるいは③右辺のみいじって=左辺になった、ドヤ□。④左辺引く右辺=0になったわ□。のいずれかのパターンで考えましょう。そして、中3で←は必須問題です。道が正方形だったり、丸みを帯びてたり・・・。どのパターンが出題されても解けるようにしておいてください。もう一度言います。この手の問題は必ず出ます。出てましたよ。※証明問題で注意しなけれないけない、いや絶対にやっちゃダメなことがあります。それは、証明する式をいきなり使ってしまうことです。だって、証明しなけれないけないものだから、その時点ではまだ=だとは言えてない。それを=だとして展開するのは、しちゃいけないことだよね。証明してから初めて堂々と使いましょうという意味です。覚えておいてください。→大学入試では、(1)で証明させて、(2)ではその式を使って解いてくださいね。という優しい誘導問題がよく出題されます。この流れを知ってるだけでアドバンテージです。