数Ⅱ
数Ⅱ · 04日 4月 2024
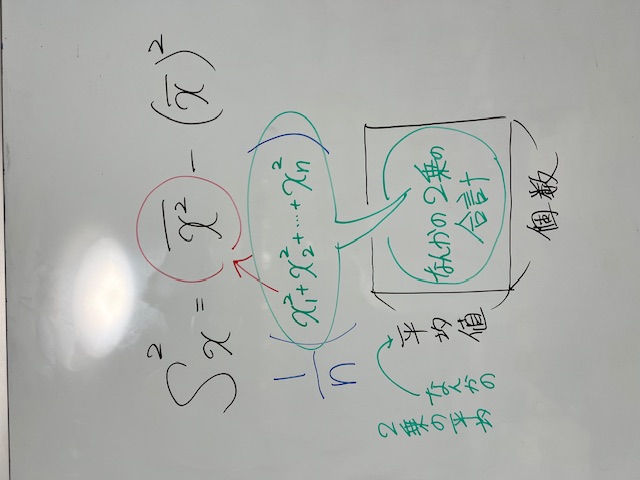
分散のここの部分。わかる生徒には問題なく理解できる部分ですが、数学が苦手な生徒さんは、ここで手が止まります。2乗の平均値の姿が、イメージができないんです。なら、絵に描いちゃおうか。なんかの2乗の合計がここになるね。なんかの2乗の合計なんか、どうやって計算するのさ？だいたい、データの数値でてないのに。そうなんです、出てないんです・笑。なので、逆に、分散値からなんかの2乗の合計値を導き出すことができるんです。でしょ＾＾ じゃぁ、同じように考えれば、普通の平均からは「なんかの1乗の合計」がわかるということだね。平均からは1乗の合計、分散からは2乗の合計と考えれば簡単に思えてくる・笑。
数Ⅱ · 24日 3月 2024
二項定理、それと似た多項定理ってのもあるけど、これなんだっけ？正直いつ使うのかも含めよくわかんないよね。じっと眺めてると、あることに気が付きます。（カッコの中身）は、二つの物の足し算になってます。a + b とか、教科書によっては x + y とか。つまり、あるものとあるものの和の形になってて、それをn乗してます。まぁ、見たまんま言ってるだけですがw。でも、私はこれに気が付いちゃったので、このあとがとても楽になりました。いいですか、あるものとあるものの和のn乗ですよ。大事だから二度言いました。この型を見たら二項定理使えるかもと思い出そう。教科書では、このあと右辺にはＣの足し算がズラズラ続いていきます。 つまり、コンビネーションの和では、二項定理を使うんですね。そう思うと、二項定理ちょっぴり身近に感じてきませんか。2つで二項定理だから、2つより多い3つ以上の場合が多項定理になるのか。なるほどと納豆。これで、謎のアルカタマリ^nを見たら、二項定理をつかっていきましょう。
数Ⅱ · 18日 3月 2024
(4次式)÷(2次式)の最小値を求めよ、なんて言われたらどうしていいかわかんないよね。しかもエックスはわざわざ実数とか書いてある・・・無理数の範囲まで広げると解けますよ、って意味なのかな。いずれにせよパッと見、難しそう。塾でよく言うのは、小・中・高校生のうちは解ける問題しか出されないさ。解けない問題が出るのは大学生。だから、小中高のうちは、どうせ解けるんでしょ、と安心してある意味舐めてかかっていいから。つまり、無駄に焦る必要はない、ってこと。だって、どうせ解けるように作られてるんだから。なのでXは0以上とヒントが出てるので、今回は相加相乗平均の不等式で考えてみる。4次式割る2次式だから、うまくいけば、かけたら定数になってくれるかも。割り算して確かめてみよう。ほらね、うまくいきそうだ（嬉）。あとは計算するだけ。でも、出てきた数が最小値とは限らないよね。最後、ちゃんと最小値になるのかを確認しよう。つまり等号が成立するかどうかを。これ、大事です。これしないと、大きく減点、もしくは0点だと思います。今回のは自治医科大学の過去問でした。
数Ⅱ · 13日 3月 2024
相加相乗平均の不等式って、どんな時に使うのかを意識せずに、ただひたすら公式を暗記してませんか？実は私が高校生の頃はそうでした（苦笑）。しかも、等号成立って何？というレベルでした・爆。何も考えず、ただ暗記するのみ。数学苦手な生徒の典型。社会経験を積んだ中年になってから大学の受験勉強を始めた私は、現役時は思わなかった「なんでこうなるんだろう？本質は何？」と、今になって考えるようになったのです。なので、大人になってから再度勉強したほうが理解が深まり、正直出来るようになります。社会人に勉強お薦めです。話を戻します。相加相乗平均の不等式の意味は、比べる2数がともに正の場合は、この2数で足し算した平均値が、かけ算した時の平均値より大きくなる時もあるよ、という意味に読みとれますよね。大きくなる時もある、逆に大きくならない時、つまり＝の時は、同じ数同士の時。3と3等。これが等号成立の時。肝心の、いつ使うのって話は、足し算する2数をもしかけ算したら、なんと定数になっちゃう場合。最小値を求める時です。でも、≧の数が本当に最小値になるのかは確認しなければなりません。忘れないでくださいね。
数Ⅱ · 01日 2月 2024
高１生は、1月から数Ⅱに入ってます。コンビネーションの和は大丈夫ですか？二項定理って、暗記に頼るとなんでこうなるのかわからないまま使っちゃいますよね。しかも、順番もまちがえちゃったりして。(x + y)^n（チルダ^のnはｎ乗の意味です）って、つまり( x + y )のn乗は ( x + y ) x ( x + y ) x ・・・x ( x + y )と( x + y )とn回掛けてるわけです。そこで展開後の各項の形を考えましょう。つまり、全掛けのパターンで考えるのです。まず最初にx^nの組み合わせは1個しかありません。そりゃそうですよね。次第にxの項の個数は1個ずつ減っていきます。その代わりその減った個数分yのが追加されます。だって全部でn個の組み合わせ（かけたもの）がズラズラ出てくるわけですから。なので次に出てくるのはx^(n-1)・y^１の形の物です。これの場合の数を考えればいいんです。n個並べたときのy1個が入る場所を選んであげる。つまりnC1個分ありますね。同様にx^(n-2)・y^2なら少ないほうのyの箇所を選ぶ方が計算楽なのでnC2個だけ出てきます。