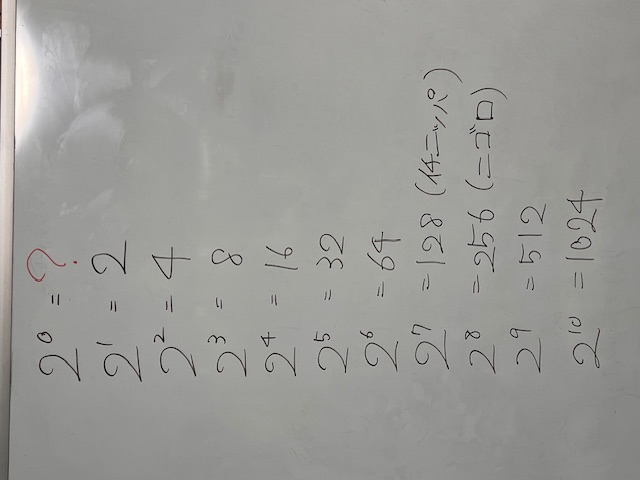中１数学
中１数学 · 19日 5月 2025
当塾では、小学生のころから、先日の2乗（平方数）の他に、2の0乗から2の10乗までも覚えるよう伝えてます。未だの場合は新中1からでも始めてください。紙に書いて貼るだけ、眺めるだけで自然と覚えますから。教える理由は2つあります。1つ目：指数を見慣れるので、指数計算を間違いません。中1で初めて指数を習った子で多い間違えは、指数をかけ算風に計算してしまいます。こうなると、この癖を抜け出すのが大変。ところが、小学生のころから指数に触れてる生徒たちは、ほぼほぼ間違いません。しかも、指数の範囲を自然数から負の整数や分数に拡張しても、すんなりついてきて理解してくれます。例えば、中3で5の3乗根2と言っても理解してくれます。２つ目：中1で累乗の数のかけ算とか割り算等の、いわゆる指数法則（公式）を見せる前に試しに解かせても、自力で解く子続出します。指数法則の(3)、分配法則みたいなやつの逆バージョン。慣れてない中学生はここができない。中3時の因数分解の難問で、もちろん高校数学でも頻出、を簡単にクリアできるようになります。いいことだらけです。覚えておいて損はありません。
中１数学 · 09日 5月 2025
昨日の解答：女子の人数は102人でした。 2乗の数、つまり平方数を
なかなか覚えきれない子は、机の前の壁に貼ってください。（と、言われても貼らない子は多いでしょう。このblogを見てくれてる保護者様、貼らせてください。お願いします。）毎日目に入ってくると、嫌でもそのうち自然と覚えちゃいますから。例えば、13の2乗=169ですが・・・この表を覚えちゃった子は、169を見ると、瞬間的に13の2乗を連想するようになります。実は、こっちのほうが真の目的なんです。平方数に気が付く力は、特に中3の因数分解の時に威力を発揮します。どのみち必要になってくるので、中1の今から覚えちゃいましょう。当塾では、早い子は小学生のころからこれを覚えさせてます。まだすぐに必要ないならやりたくない。つまり、やらない言い訳を先行させる子と、素直に行う子では、私の経験上、その後の数学の伸びは、大きく変わり、結果かなりの差が付きました。壁にただ貼るだけ。誰でも出来ます。特別なテクニックも不要。必死に暗記する必要もなし。なので、頭も使いません。一番楽で超簡単に覚えれる方法です。やらないのは勿体ないです。
中１数学 · 18日 4月 2025
(1)では、「和は0とは？」と具体的にしっかり考えようとする習慣が身についてる生徒は正解に近づけます。次に、「差は5」の「差」の意味が理解できれば解けます。問題なのが(2)です。多くの新中1生は(2)を読んだ瞬間に心が折れるでしょう。ここで、「いったい何が書てあるんだ？難しそうに見えるけど要は何なの？」と、落ち着いて本文を読み直す。既約分数とは何ぞやを説明してくれてることに気が付けば半分勝ちです。心の折れた生徒さんは、まずこのヒントが目に入ってきません。正直、半分は国語力で、数学以前の問題になります。挫けずにわかるまで読み直しましょう。必要なのは、日本語文の内容を理解しようと努力する姿勢です。難解そうに見える本文だけど、何が書いてあるのかを落ち着いて解読できた生徒だけが、正解できました。今の時点4/18で(1),(2)の両方ともすぐ解けた新中1生は、学年で5番以内に入れる可能性がある・・・でしょう。
中１数学 · 05日 4月 2025
素数って何？・・・ここで詰まる生徒さんは、「素数とは、1と自分自身以外に約数を持たない自然数のこと」です。と、スラスラ言えるように練習してください。（言い換えると、素数は2以上の自然数で、約数の個数が1と自分自身の二個だけだけのやつ）。当塾では100までの素数は語呂合わせで暗記させるので、早い子だと1時間で覚えちゃいます。新中1の入学後すぐの実力テスト：お迎えテストで素数が出たこと何度もあります。素因数に分解するときに使うアレです、と言われたら思い出す保護者様も多いでしょう。中学生になって、これらを知らないままでいると、通分、約分で手が止まるかもしれません。知っておいて損はありませんので、覚えちゃってください。中学校の教科書にも載ってるはずです。
中１数学 · 29日 11月 2024
今月、中1が1名入塾しました。方程式の利用から苦手になったそうです。当塾の中1クラスの数学は、幸い全員の進度がバラバラなんです。一人は高2レベルを、一人は中1と中2レベルを、また一人は中1の基本から復習中など。このように各自が今取り組むべき分野を個別のテキストで学習してます。私は巡回してそれらを個別に指導。つまり先日入塾された生徒さんにとって、苦手意識のある数学・方程式の利用を個別指導で克服できるNICEなタイミングでした。中1の発展系の問題になると、全員が個別問題の手を止めて、同じ問題（中1）に取り組みます。全員参加型になると、個別ではつい出がちな気持ちの緩みを見せられません。周りの生徒も必死に取り組んでるため、つられて自分も解こうと前向きになります。これが物凄い成果を生み出します。本当に目に見えて結果に現れます。これが半分個別指導です。伸び悩んでる生徒さんに本当にお薦めです。先日の遺愛中のオープン模試でも保護者様が驚くくらい良い結果が出ました。中1の数学：半分個別指導中は、平均点ちょい上レベルから抜け出したい生徒さんにピッタリのクラスと言えるでしょう。
中１数学 · 13日 11月 2024
中1の方程式の利用です。この手の問題で通常は、女子の生徒は何人ですか？とか、男子の生徒数を求められるので、それらをＸ（ｴｯｸｽ）にすればいいんです。ですが、今回は中学1年生全員で何人ですか？と問われてます。ここをどうクリアするか。まずは、解説を見ないで自分の手を動かして解いてみてください。考えれば考えるほど頭を使うので、あなたの偏差値は上がるはずです。ヒントは本文中に隠されてます。いや、隠してません、さらしてますwww。そうです、いつもならないのに、わざとらしく書いてある箇所を見つけましょう。その条件の下で解いてくださいね、この条件を必ず使うんですよ、という優しいヒントですから。
中１数学 · 06日 11月 2024
2台の列車がすれ違う。状況はイメージできるけど、数学だから式で表わしたい。どうすればいい？とりあえず今回は、右向きに進んでる急行に私（自分）が乗ってると仮定して、普通列車を（相手）として考えてみよう。お互いが反対方向に進んでるからややこやしい。なので自分を固定（動かない）して、相手の速度（相対速度＝自分から見た相手の速さ）を考えてみる。（速度の）違い＝差だよね。差は引き算で求めるはず。なので、自分ひく相手でもいいし、今回は自分が右方向（数直線で考えるとプラス方向）、相手は反対向きに進むからマイナスとしよう。相手ひく自分は=-35になる。⊖が付くということは「自分とは逆方向に進んでる」ということだよね。つまり自分と相手は35m/sの速さで離れていくともいえる。これでキハジの速さが分かった。あとは、ただ計算するだけのゲーム。普通列車の長さを求めるわけだから、長さをＸ（エックス）として計算してあげよう。
中１数学 · 21日 2月 2024
中1の数学第五章はコンパスでの作図と扇形の面積です。冬休み中、これでもかというくらい塾でコンパスと扇形の練習をしました。その結果・・・なんと全員が平均点(50点代)を大きく上回る70点代をとってきたのです。今まで平均点以下の生徒もいます。いや、平均点を大きく下回ってた子もいます。あの、平均点以下だった生徒たちが、下手をすると80点に手が届きそうな点数なんです。今回爆上げを体感した生徒達は、復習の威力を思い知ったことでしょう。ある生徒は、授業後に習った個所をノートを見て確認しながら帰り支度をしてました。その子のこんな姿初めて見ました。いや、帰り際にノートを見返し復習した生徒は、開塾以来初めてです。この子は、中学の最初の実力テストは理科も数学も全部平均点以下。でも、次第に前向きさが出てきたんです。確かに、この生徒さんは理科も爆上げしてました。次の期末テストも楽しみになってきました。
中１数学 · 22日 11月 2023
これを初見でスラスラ解ける小5は、大したもんです。うちの小5は、時間のところの罠に気が付かず間違えました・笑。普通、ココ間違えますよね。寧ろ、ここを10/3時間に代えて計算する小5生は、かなり勉強してます。凄いです。当塾では、時速が出たら km/時、もしくは km/h と書かせてます。この表記に慣れると、kmのときは、単位は時間で考えることを覚えます。（分じゃない）。ちなみに50km/時を50km/分と書いてしまったら、1分間に50kmもすすむのかよ（爆笑）。どんだけ速いのよ、身体もたないじゃん。1時間で日本の端からは端まで(3000ｋｍ)行けちゃうから、飛行機より速いぜ！なので分速ならメートルレベルだよね。m/分、もしくはm/mね。だから秒速のときも1秒間に進む距離だから普段の生活で考えれば、せいぜいメートルくらいが無難だよね。もし1時間単位で考える時速なら、がっつりすすめるkmで。分や秒で考える時は、そんなに進めないからメートル（m）で考えるんだよ。これで、式を建ててる最中に間違えてしまっても、違和感覚えるはずです。そこで間違に気が付いて直せればいいんです＾＾。