中３数学
中３数学 · 10日 9月 2025
私は、基本対称式で解きましたが、これを使わずに、①の分子を普通にaの2乗、bの2乗を計算しても同じ答えを導けます。中学のうちから「対称式」「基本対称式」という用語に慣れていると、高校数学でもよい点数を取れるでしょう。今回のポイントは、文字を含んでるけど「分数の足し算」ができますか？というところでした。分数の足し算は小4くらいで習うんだっけ？本問の答えは 14 でした。ね、意外と簡単だったでしょ^^ 解けなかった人の半分以上は「文字のついてる分数の足し算で止まってしまった」のではないでしょうか。文字があってもビビらずに、ここを躊躇なく計算し始める子は、基本が身についてますので大丈夫です。まずは、自分の持ってる力で、進めれるところまで計算してみましょう。いきなり結果を求めちゃダメ。途中でうまくいかなくなる時がきたら、その場で考え直せばいい。手が詰まったら、自分で実験してみよう。（自分にとって）難問だと感じたら、簡単な数字に置き換えて、考えて直してみよう。大切なのは、焦らないことです。
中３数学 · 09日 9月 2025
最初に、どういう手順で解いていこうかだけを考える。答えを求めれなくてもOK。中3に限らず、←の問題を小・中学生のうちに「躊躇なく解き始められる」生徒さんは、とりあえず一安心です。基本は身についてます。今後も、ペースを落とさず数学を楽しんで勉強し続けてください。また、左の問題を、今の学年で「基本対象式で」と考えたあなたは、もっと素晴らしい。上手くいけば、中学だけでなく、高校でも数学は学年10番以内には入れる可能性あります。ソースは、昨年の中3。←を「代入の力業ではなくて、基本対象式で解いたその生徒」は、先日の高校のテストで学年6番でした。ちなみに、先程自習に来てた中3君にやらせてみたら・・・この子は途中から力業（代入法）で解いてました。もちろん正解ですのでこのやり方でも問題ありません。今後、基本対称式で、も身につけたら更に順位UPするでしょう。あっ、そうだ。今度、当塾の小6や中1、中2でルートの計算ができる生徒達にも出題してみます。あの子たちは、どうやって挑むんだろう？手が止まるのか。それとも躊躇なく◎分し始めるのか。ちょっと楽しみです。
中３数学 · 06日 9月 2025
問題を読み終わって、考える事は・・・解法の手順を考える事です。つまり、大雑把に道筋を決めるのです。それが見えたら、あとはそれに従って進めていけば良いのです。数学が苦手で、手が止まってしまう生徒さんは、この
「解放の手順を」全く考えてないからです。この段階では、まだ計算なんかしなくていいんです。むしろ、すんな！です。
でも、数学が苦手な生徒さんは、まず計算ありきなんです。そして立式できず、手が止まります。計算なんかしなくていいと思えば気が楽になりませんか。順番を考えるだけ。そのあとに、じゃぁ今からどうやって計算するのよ？おら知らね。で、いいじゃないですか。わからないからしょうがない、ここで頭使って考えましょう、なんです。今回は、おしゃれな解き方でやってみっか。と思い出せた人は運が良い。答えは 4 です。あってましたか？
中３数学 · 03日 9月 2025
この手の問題を解く時、あなたはどうやって解きますか？普通は、何も考えずに、そのまま代入を選択するでしょう。それで解けますので問題ありません。ただ、ルートの計算が出てくるので、数学が得意でない生徒さんにとって、ちょっとだけハードル高く感じちゃいますよね。そうなんです。ルートがなんとなく嫌なんです。じゃぁ、その「嫌なルート」をいつまでも残しておくのは得策じゃない。嫌なもんは、なるべく見たくないので消しちゃうことを考えましょう(^^)。右辺はルート（無理数）だけにします。おしゃれ編、1行目。あとは、ルートをなくしてあげてお終い。何も考えずに、公式通り計算するだけ。つまりただの手の運動です。下から2行目の緑色の式を得ました。あとは辻褄合わせるために両辺に+1するだけ。答え 6 になりました。めでたしめでたし。私（先生）は、いつもこの方法で解いてます。慣れると超ラクなので、お薦めです。次回は、この手の練習問題です。
中３数学 · 30日 8月 2025
CDEFが平行四辺形とわかったんで、あとは相似の問題になります。一辺の長さは何でもよいので、とりあえず「1」としましょう。これが一番計算しやすいです。そして対角線の長さはわからないので「X」としときます。底角が〇1個の△ABCと△AFBを比べてあげて、比例式から対角線xを解の公式で求めてください。ね、中学生でも求められたでしょ(^^)。ここで、注意。対角線は長さなので「－（マイナス）は、あり得ません」。試験では、しっかり記述てくださいね。ないと減点、いや不正解になるかもしれません。当塾では、口酸っぱくいってます・笑。この癖は、中学生のころからしっかり身につけておきましょう。高校数学、大学入試では致命傷になりますので。そして、この 1 対 ( 1 + √5 ) / 2 が黄金比です。ちなみに、身近では、名詞のサイズやたばこの箱も黄金比です。車のエンブレムだったり、ミロのビーナスのへそ上と下の上下比も。絵では、モナ・リザ、富嶽三十六景・神奈川沖浪裏も黄金比でしたね。
中３数学 · 28日 8月 2025
附属中の生徒から黄金比の質問がありましたので一緒にお勉強しましょう。そういえば黄金比、15年位前に、教育大（函館校）の入試で出た記憶があります。さて、北海道函館には五稜郭があるので、親しみ持てますね。正五角形（Pentagon）の一辺と対角線の長さの比を考えてみます。とりあえず、正五角形に対角線(青)を引いてみると、アサヒビールのマークが出てきました。これは、五芒星というんだよ。（ちな六芒星はダビデの星ね）。よく見ると、五芒星の中にも「小さな正五角形風(緑色斜線部)」なのが見えるね。これ、本当に正五角形かな？自分で、証明してみよう。中学生なので、角度で考える。大島学習塾に入ると、小6や中1で全員が一番最初に必ず習う事があったね。「△の2つの内角の和は、もう一つの外角になる。」これを使えば解けそうだ。・・・中略・・・無事、この小さいのも正五角形であることがわかりました。あと、角度：錯覚と同位角から、この対角線ACと辺DEは平行であることもわかったね。なんか、これ使えるかも。もしかして、ここCDEFは平行四辺形なのか。
中３数学 · 27日 6月 2025
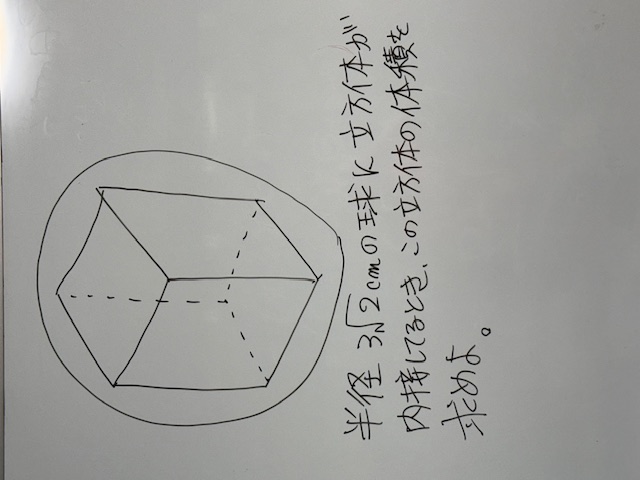
一瞬、「はっ？」と戸惑いますが、冷静に考えると意外とわかっちゃったりします。実際、塾の中1に見せたところ、それほど絶望せず、すぐに自分で考え始めました。問題文を読み直すと、半径が与えられてて、しかも球に内接しているのは立方体です。これらのことから中1生女子は、あることに気が付きました（えらい！）。あとは、中3・高1の三平方の定理を知っていればすぐに解けます。とりあえず、適当に内接してる接点に名前（アルファベット）をふってあげましょう。そうすると計算しやすくなりますね。今回のポイントは、問題を見た時に心折られず、まずは「どういう状態なのか」を冷静に考えてみる事でした。まずは自分の力で挑戦してみてください。