数Ⅱ

数Ⅱ · 07日 7月 2025

まず与式の（　）の2乗は、暗算ではなく、展開の公式をスラスラ言えるようにしておきましょう。ここで時間短縮できます。次に積分区間に着目すると、なんとy軸に対して線対称の位置。つまり被積分関数を偶関数と奇関数に分けたら超ラクできることを思い出した人が勝ちです。ここが「は？」の人は偶関数・奇数関数をしっかり復習してください。3行目まで来れましたか。次は、ただの積分です。５行目まで辿り着けた人はかなり良い。あとは最小値を求めましょう。変数が2個あります。aとbが好き勝手に動き回ります。どうしましょう？片方固定の予選決勝風で。頑張って計算しておしまいです。今回は計算問題の練習でした。あってましたか？

数Ⅱ · 05日 7月 2025

積分の問題ですが、計算の練習でもあります。皆さんならどう解きますか？　とりあえず、そのまま計算しても解けそうです。ただ、面倒くさそう。と、いうことは工夫して解きましょうという意味です。今日のヒントはここまで。頑張って自分の手を動かして解いてみてください。ちなみに左の記号は「インテグラ」です。覚えてますか？懐かしいですね。これは積分区間を示してます。よく見ると、S（エス）を縦に伸ばした形に見えませんか^^。そうなんです、Sなんです。S→SUM。エクセルの関数で出てくるSUMといえば合計です。つまり積分って合計なんです。と思えば、少しだけ身近に感じますよね。積分では、面積を求めてたのです。人類は、エジプト文明の頃に直角の正方形、長方形だけでなく、曲がった場所の面積を求めようとしたのです。ナイル川が氾濫し、自分の土地の境界線がわからなくなった・・・曲線を含んだ境界線のある土地の面積を計りたい。人は知恵を絞って考えたんです。人って凄いですよね。紀元前3000年前からこんなことしてたなんて。なのでありがたく先人の知恵を使わせていただきましょう。一生懸命私たちも勉強しましょう。

数Ⅱ · 03日 3月 2025

C1の接線とC2の接線が一致するはずなので、それぞれの接線を求めてから比べて解いていくと結構面倒くさいですよね。なので、もう一つの曲線C2と接するということは、接線と連立させたときに重解を持つということになるので、これと組み合わせたほうが楽に解けます。求める部分の面積の出し方は、公式を使うかどうかは皆様次第。お好みの方法でどうぞ。ちなみに最後は偶関数奇関数の性質を使おうかなと思いましたが、うまいこと因数分解できたので、これは優しいお導きだと捉え、そのまま素直に積分しました。いつも言ってますが、まずは自分の手でチャレンジしてみてください。そして、復習。これを繰り返していけば確実に偏差値上がっていきます。

数Ⅱ · 22日 2月 2025

この手の問題、通常は加法定理で解くと思いますが、もし位相の中身はﾊﾟｲ/4つまり45°以下に変えられるのを知ってるともう少し楽に解けます。本問は、わざとらしく全ての分母が12です。これはﾊﾟｲ/12に揃えるんだよ、という優しいメッセージだと思いますので、素直に乗りましょう。サイン⇔コサインの変換は単位円を用いてもよいのですが、私はグラフ派です。小さくメモしておきますので参照してください。ﾊﾟｲ/2から考えればいいので本当にラク。お薦めです。ここまできたら、あとは書き替えるだけ。なんと( カッコ )の中、計算したらZEROになっちゃいました。焦りますが、何度見直してもZEROです。なので、答えは 0 になりました。みなさん、いいですか。板書のミスに気が付きましたか？塾の授業でもよく言ってます。うつすだけじゃだめだよ。自分の頭で考えて、自分の手で書いてみる。その結果、板書と一緒ならいいし、板書が違う、板書が間違えてることに気が付く時もあるからね。これ重要だよ。ちゃんと自分の頭で考えて解きなおしてみる。これやることで偏差値確実に上がります。信じて実行してください。

数Ⅱ · 01日 2月 2025

問題文に「調べよ」と書いてあるから、答えは場合分けして出すんだよというふくみです。となれば、何について場合分けするんだろう？と考えましょう。問題文には文字aが出てます。多分これですね。まずは、グラフで視覚的に考えたほうが分かりやすいはず。3次関数に傾き4の直線を当てていって、その時のy切片aを求めていくのか。でも、それも面倒くさいな。なら、ちょっと工夫したら、もう少しラクちんに見れそうな型にしてあげよう。どうすればいいか、よくわかんないけど、とりあえずこの2式を合体させて、異なる実数解の個数としてみようか。すると、いい感じに定数のaだけ浮いてきた。これを右辺に移項して、定数分離だと気が付いた人は勝ち。あとは教科書の練習問題を解くようにグラフを書いてお仕舞。定数分離様ありがとう。理科大の過去問でした。

数Ⅱ · 31日 12月 2024

与式を見た瞬間、「何これ？嫌だ」とひいちゃいませんでしたか？そこが出題者の作戦と捉えて、「私は騙されませんよ、見やすく書き直せばいいんでしょ」と、斜に構えて挑んでください。64みたら2^6。81見たら3^4と思い出せたら勝ちです。あとは指数法則にのっとって変形していきます。ほらね、２行目、更に3行目はかなりシンプルになりました。あとは底を今回は2に揃えて計算しましょう。最後の4行目、5行目は惑わされないでくださいね。小学生の分数の問題です。

数Ⅱ · 14日 10月 2024

10/12の問題の続きです。2次関数の最大値、最小値ですからグラフで、ですよね。(1)でtの定義域を求めてあるので、平方完成さえできれば、もう勝ちです。θの値を求められなかった人は、何度も練習してください。でも、図に描いたら問題なく解けるようになります。ほらね。頭の中だけで解こうとするから時間がかかるんです。はい、お疲れ様でした。

数Ⅱ · 12日 10月 2024

よくある数2：三角関数の問題です。この手の問題はスラスラ解けるようにしといてください。では、始めます。与えられた式は２θ（2シータ）、θ（シータ）と位相が揃ってません（汗）。なのでまずは揃えてあげたいですね。今日の(1)は、そのためのやさしい誘導です。この t = sinθ + cosθ を見たら、「2乗」したくなるあなたは理系ですwww。文字tと置いたので・・・はい、忘れてはいけないのは　新しい文字の定義域です。後回しにするとつい忘れちゃう受験生多いので、すぐ書いときましょう。これで(1)は終了です。次回は(2）です。

数Ⅱ · 04日 10月 2024

分数で、括弧があって、更に指数も付いてて・・・なんかいまいち綺麗じゃないよね。問題文では「簡単にしなさい」だから、つまり「いきなり計算する以前に、きっと約分できるんだろうな」と考えてみましょう。あとは、頑張って「このあと約分できるようにイメージして、分子と分母の型を揃えてあげるんです」。答え、なんか今一スッキリした型じゃなかったですね・www。まぁ、こんなこともあります。

数Ⅱ · 26日 9月 2024

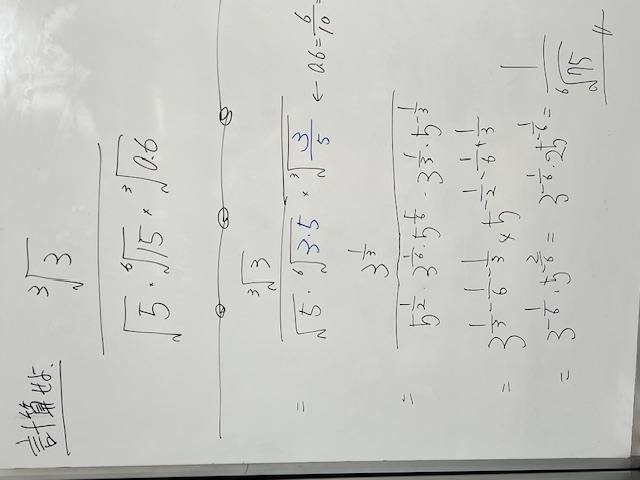
This is the question about calculating radical roots. Simplify the following expression. If the answer is a fraction, you do not need to rationalize the denominator. First, try solving it yourself without looking at the explanation from the middle part onwards. If you notice that it is made up of only 5 and 3, you win.